直角三角形的斜边如何计算？

在解决直角三角形问题时，斜边的计算无疑是一个基础且关键的部分。直角三角形的斜边，作为连接直角三角形两个直角顶点的边，具有独特的性质和计算方法。当我们掌握了一些关于直角三角形的基本知识和计算公式后，便能轻松应对各种涉及斜边长度求解的问题。

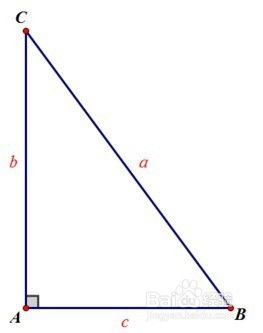
直角三角形的基本概念涉及到其三个角和三条边。其中一个角为90度，称为直角，而另外两个角则为锐角或一个锐角和一个钝角（但在我们的讨论中，主要关注直角三角形中均为锐角的情况）。三条边分别为直角边（两条）、斜边（一条）。斜边总是直角三角形的最长边，它连接了直角顶点与另外两个顶点。

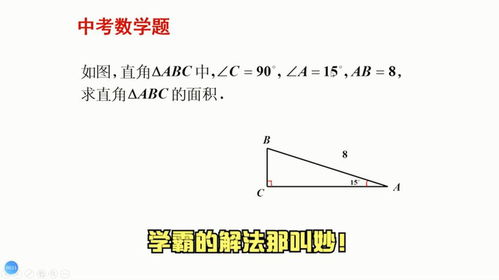
计算直角三角形斜边长度的最常用的方法是通过勾股定理。勾股定理是一个在数学、工程及物理学等多个领域有着广泛应用的定理。该定理指出，在一个直角三角形中，斜边的平方等于两条直角边的平方和。用数学公式表示即：c² = a² + b²，其中c表示斜边，a和b分别表示两条直角边。

这个定理的证明过程涉及多种方法，其中一种较为直观的方法是几何法。假设我们有一个直角三角形，以及两个与其相似的、边长比例一致的较小直角三角形。将这两个小三角形分别置于大三角形的两个直角边上，使得它们的斜边与大三角形的直角边重合。随后，我们可以发现，通过调整这两个小三角形的位置，可以将它们组合成一个正方形，其面积恰好等于大三角形的斜边所构成的正方形的面积。根据面积的等式关系，我们可以推导出勾股定理的公式。

此外，还有其他方法，如代数法、向量法等，可以用来证明勾股定理。代数法通过设置坐标系并应用坐标几何的原理来推导；向量法则利用向量的数量积和模的性质来证明。虽然这些方法的具体过程各不相同，但它们最终都指向了相同的结论，即勾股定理的成立。

掌握了勾股定理后，我们可以轻松求解直角三角形斜边的长度。具体操作时，首先需要测量或已知两条直角边的长度。然后，根据勾股定理的公式，将两条直角边的长度分别平方后相加，再对得到的和进行开方运算，即可求得斜边的长度。例如，如果直角三角形的两条直角边长度分别为3和4，那么斜边的长度可以通过计算√(3² + 4²) = √(9 + 16) = √25 = 5来得出。

值得注意的是，在实际应用中，直角三角形斜边的计算可能会涉及更多的变量和复杂性。例如，当已知的信息不是直角边的长度，而是角度或其他边长与角度的组合时，我们需要运用三角函数的知识来求解。三角函数如正弦（sin）、余弦（cos）和正切（tan）等，为我们提供了在不同情境下计算直角三角形边长的方法。正弦等于对边除以斜边，余弦等于邻边除以斜边，正切等于对边除以邻边。通过这些关系式，我们可以在已知某些边长和角度的情况下，推算出斜边的长度。

在利用三角函数计算斜边时，我们通常需要根据已知条件选择一个合适的函数公式。例如，如果我们知道一个锐角的大小和它的对边长度，就可以通过正弦函数来计算斜边。这是因为正弦函数的定义正好涉及到了对边和斜边的比值。同样地，如果我们知道邻边长度和角度，就可以使用余弦函数；如果知道对边和邻边的比值（即正切值），则可以使用正切函数。需要注意的是，在选择使用哪个三角函数时，应确保所选函数中的变量（如角度和边长）与已知条件相匹配。

另外，在实际应用中，我们还可能会遇到一些特殊情况下的直角三角形斜边计算问题。例如，在解决三维空间中的直角三角形问题时，可能需要利用空间向量的方法或立体几何的知识来进行计算。此时，斜边的计算可能不再简单地依赖于勾股定理或三角函数，而是需要更复杂的方法和公式。

然而，无论情况多么复杂，解决直角三角形斜边计算问题的核心思想都是不变的：那就是通过利用已知的边长和角度信息，结合勾股定理、三角函数等数学工具，来推导出斜边的长度。这个过程既是对数学知识的应用，也是对逻辑思维和问题解决能力的锻炼。

在掌握了这些基本概念和方法后，我们就可以在解决实际问题时灵活运用它们了。无论是建筑设计中的结构分析，还是物理学中的运动学研究，甚至是日常生活中的简单测量和计算，都离不开对直角三角形斜边长度的求解。因此，熟练掌握直角三角形斜边的计算方法，对于我们提升数学素养、解决实际问题具有重要意义。

总的来说，直角三角形斜边的计算是一个涉及多种数学知识和方法的复杂过程。通过理解和应用勾股定理、三角函数等基本概念和工具，我们可以轻松应对各种情况下的斜边计算问题。同时，这个过程也锻炼了我们的逻辑思维和问题解决能力，使我们能够更好地运用数学知识解决实际问题。