标准误的计算方法是什么

当我们谈论统计数据分析时，标准误（Standard Error）是一个至关重要的概念。它不仅是衡量抽样误差的尺度，更是评估统计推断可靠性的重要工具。那么，标准误的计算公式是什么呢？让我们深入探索这个统计学的核心概念。

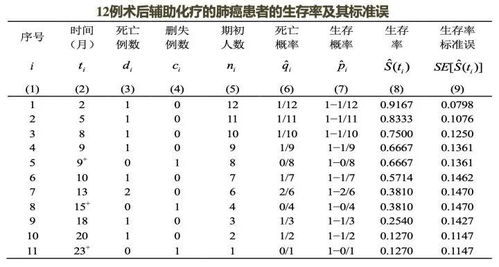
首先，标准误的定义是什么？简而言之，标准误是用来衡量样本统计量与总体参数值之间接近程度的尺度。换句话说，标准误越小，样本统计量（如样本均值）与总体参数（如总体均值）的值就越接近，样本对总体的代表性就越强，用样本统计量推断总体参数的可靠度就越大。因此，标准误在统计推断中扮演着举足轻重的角色。

那么，标准误的计算公式具体是什么呢？答案是：标准误等于标准差除以样本大小的平方根（N的根号）。公式表达为：标准误=标准差/√N。这里，标准差是衡量数据离散程度的统计量，而样本大小则反映了样本的容量。通过这个公式，我们可以计算出样本均数的标准误，进而评估样本均值作为总体均值估计的可靠性。

那么，标准差与标准误之间有何异同呢？首先，两者的定义不同。标准差是单次抽样得到的数据集的离散程度度量，它衡量的是各个数据点与数据集均值之间的偏差。而标准误则是多次抽样得到的多个样本均值的离散程度度量，它衡量的是不同样本均值之间的偏差。换句话说，标准差描述的是数据集的内部变异性，而标准误描述的是样本均值之间的变异性。

其次，两者的应用也不同。标准差主要用于描述数据集的内部变异性，帮助我们了解数据集的分布情况和离散程度。而标准误则用于评估样本均值作为总体均值估计的可靠性。当我们想要根据样本数据推断总体参数时，就需要考虑样本均值的变异程度，即标准误。标准误越小，说明样本均值之间的变异越小，样本均值越接近总体均值，因此用样本均值推断总体均值的可靠度就越大。

此外，标准误还有一个重要的特性，即它反映了样本均数之间的变异程度。在统计学中，我们通常认为样本均数比单个数据点更能代表总体。然而，不同的样本均数之间也会存在一定的变异。这种变异程度就是标准误所衡量的。标准误越小，说明不同样本均数之间的差异越小，样本均值越稳定，因此用样本均值进行统计推断的可靠性就越高。

为了更好地理解标准误的计算公式和应用，我们可以通过一个具体的例子来说明。假设我们有一个包含100个数据点的数据集，我们希望根据这些数据点来估计总体的均值。首先，我们可以从数据集中随机抽取一个样本，计算该样本的均值。然后，我们可以多次重复这个过程，得到多个样本均值。接下来，我们可以计算这些样本均值的标准差，即标准误。通过比较标准误与数据集的标准差，我们可以评估样本均值作为总体均值估计的可靠性。如果标准误较小，说明样本均值之间的变异较小，用样本均值推断总体均值的可靠度就较高。

在实际应用中，标准误的计算公式有着广泛的应用。例如，在医学研究中，我们经常需要根据样本数据来估计某种药物的疗效或副作用。此时，我们就可以利用标准误来评估样本均值作为总体均值估计的可靠性。如果标准误较小，说明样本均值之间的变异较小，用样本均值推断药物疗效或副作用的可靠度就较高。同样地，在市场调研、社会科学研究等领域中，标准误的计算公式也发挥着重要的作用。

此外，值得注意的是，标准误并不是测量值的实际误差或误差范围。它只是对一组测量数据可靠性的估计。因此，在解读标准误时，我们需要谨慎对待。一方面，标准误可以帮助我们评估样本均值作为总体均值估计的可靠性；另一方面，我们也需要结合其他统计量（如置信区间、P值等）来全面评估统计推断的可靠性。

最后，需要强调的是，标准误的计算公式虽然简单，但其背后的统计学原理却十分深奥。在实际应用中，我们需要根据具体的研究背景和目的来选择合适的统计方法和模型。同时，我们也需要对统计结果进行谨慎的解读和评估，以确保统计推断的准确性和可靠性。

总的来说，标准误的计算公式是统计学中的一个重要概念，它用于衡量样本统计量与总体参数值之间的接近程度。通过计算标准误，我们可以评估样本均值作为总体均值估计的可靠性，进而为统计推断提供有力的支持。在实际应用中，我们需要根据具体的研究背景和目的来选择合适的统计方法和模型，并谨慎解读和评估统计结果。只有这样，我们才能充分利用标准误的计算公式来推动统计学的发展和应用。