如何求解函数的定义域和值域?
在数学学习中,掌握定义域和值域的求解方法是至关重要的。这不仅能帮助我们更好地理解函数的性质,还能在实际问题中灵活运用。下面,我们就来详细探讨一下定义域和值域的求解方法。

首先,我们需要明确什么是定义域和值域。函数的定义域是指函数中自变量x的取值范围,即所有能使函数有意义的x的集合。而函数的值域则是指函数值的集合,即函数在定义域内所有可能取到的y值。

一、定义域的求解方法

1. 对于基本的初等函数,如一次函数、二次函数、指数函数、对数函数等,我们可以根据函数的解析式直接确定其定义域。例如,对于一次函数y=kx+b(k、b为常数),其定义域为全体实数R;对于二次函数y=ax^2+bx+c(a、b、c为常数,a≠0),其定义域同样为全体实数R;对于指数函数y=a^x(a>0且a≠1),其定义域也为全体实数R;而对于对数函数y=log_a x(a>0且a≠1),其定义域则为所有正实数,即x>0。

2. 对于分式函数,我们需要保证分母不为零,即解不等式分母≠0,从而得到函数的定义域。例如,对于函数y=1/(x-1),我们需要解不等式x-1≠0,得到x≠1,所以该函数的定义域为{x|x≠1}。
3. 对于根式函数,我们需要保证被开方数大于等于零,即解不等式被开方数≥0,从而得到函数的定义域。例如,对于函数y=√(x-1),我们需要解不等式x-1≥0,得到x≥1,所以该函数的定义域为[1,+∞)。
4. 对于复合函数,我们需要先求出内层函数的定义域,再根据内层函数的值域求出外层函数的定义域,从而得到复合函数的定义域。例如,对于复合函数y=log_2(3x-1),我们需要先求出3x-1>0的解集,得到x>1/3,所以该复合函数的定义域为(1/3,+∞)。
5. 对于抽象函数,我们需要根据题目给出的条件或关系式,结合函数的定义和性质,求出函数的定义域。例如,若函数f(x)的定义域为[0,1],则函数f(2x+1)的定义域需要满足0≤2x+1≤1,解这个不等式组得到-1/2≤x≤0,所以函数f(2x+1)的定义域为[-1/2,0]。
二、值域的求解方法
1. 对于一次函数y=kx+b(k、b为常数),当k>0时,函数的值域为全体实数R;当k<0时,函数的值域也为全体实数R,但此时函数是单调递减的。对于具体的k和b值,我们可以通过计算得到函数在定义域内的最小值和最大值(如果有的话),从而确定函数的值域。
2. 对于二次函数y=ax^2+bx+c(a、b、c为常数,a≠0),我们可以通过配方法将其化为顶点式y=a(x-h)^2+k的形式,然后根据a的正负和顶点的坐标来确定函数的值域。当a>0时,函数的值域为[k,+∞);当a<0时,函数的值域为(-∞,k]。特别地,当b^2-4ac=0时,二次函数有一个重根,此时函数的值域为{y|y=c-b^2/(4a)}。
3. 对于指数函数y=a^x(a>0且a≠1),当a>1时,函数的值域为(0,+∞);当0
4. 对于对数函数y=log_a x(a>0且a≠1),其值域为全体实数R。这是因为对数函数是指数函数的反函数,而指数函数的值域为(0,+∞)(当a>1)或(0,1)(当0
- 上一篇: 标准误的计算方法是什么
- 下一篇: 轻松掌握:如何开启445端口
-
 如何求函数的值域常用的方法有哪些?资讯攻略12-04
如何求函数的值域常用的方法有哪些?资讯攻略12-04 -
 探索函数值域的多样化解题妙招资讯攻略11-04
探索函数值域的多样化解题妙招资讯攻略11-04 -
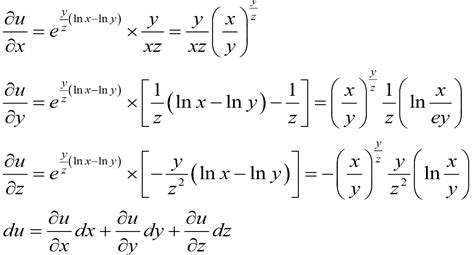 如何求解全微分资讯攻略11-16
如何求解全微分资讯攻略11-16 -
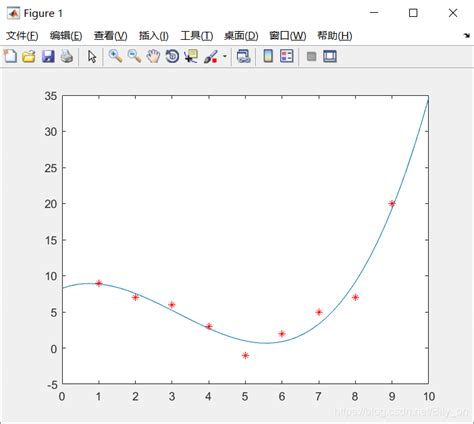 如何在MATLAB中高效定义函数?3种实用方法揭秘!资讯攻略12-05
如何在MATLAB中高效定义函数?3种实用方法揭秘!资讯攻略12-05 -
 掌握Excel技巧:轻松运用GAMMA.INV函数资讯攻略11-29
掌握Excel技巧:轻松运用GAMMA.INV函数资讯攻略11-29 -
 MATLAB中如何使用length函数?资讯攻略11-29
MATLAB中如何使用length函数?资讯攻略11-29