轻松掌握:如何计算扇形面积
在几何的世界里,扇形以其独特的魅力和实用性占据着重要的位置。无论是设计精美的蛋糕、计算风力发电的效率,还是探索宇宙的奥秘,扇形面积的计算都是不可或缺的一环。你是否也曾好奇,如何轻松掌握这一技能,让扇形面积的计算不再成为你的困扰?今天,就让我们一起揭开扇形面积的神秘面纱,用简单易懂的方法,带你走进扇形的奇妙世界。
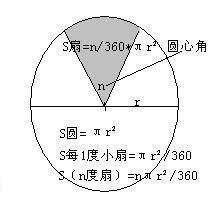
首先,我们需要明确什么是扇形。扇形,简单来说,就是圆的一部分,由两个半径和它们之间的圆弧围成。想象一下,你手中拿着一个完整的圆,然后用一把神奇的剪刀沿着某条弧线剪开,保留下来的那一部分就是扇形。扇形不仅拥有优雅的形态,更在日常生活和科学研究中发挥着巨大的作用。

那么,如何计算扇形的面积呢?这里有两种主要的方法:一种是利用扇形圆心角的大小来计算,另一种则是通过扇形的弧长来求解。无论你选择哪种方法,都需要先掌握一些基础的概念和公式。
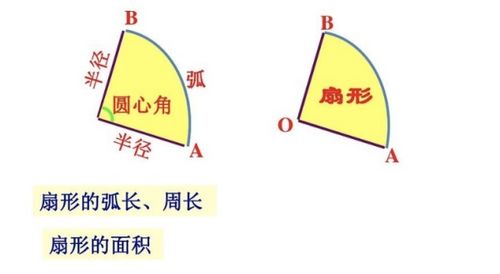
方法一:利用圆心角计算扇形面积
圆心角,就是扇形所对的圆的中心角,通常用度数来表示。一个完整的圆有360度,因此,扇形的圆心角介于0到360度之间。扇形面积与圆心角之间有着密切的关系,这个关系可以用一个简单而强大的公式来表达:扇形面积 = (圆心角/360) × π × r²。
这里,r代表扇形的半径,π是一个常数,约等于3.14159。这个公式告诉我们,只要知道扇形的圆心角和半径,就可以轻松地计算出它的面积。
举个例子,假设我们有一个圆心角为90度,半径为5厘米的扇形。要计算它的面积,我们只需要将圆心角90度除以360度,得到1/4,然后乘以π(约等于3.14)和半径的平方(5²=25)。所以,扇形面积 = (1/4) × 3.14 × 25 = 19.63平方厘米。
方法二:利用弧长计算扇形面积
除了圆心角之外,扇形的弧长也是计算面积的一个重要参数。弧长,顾名思义,就是扇形所对的圆弧的长度。它与圆心角和半径之间有着密切的关系,公式为:弧长 = 圆心角(以弧度为单位) × r。
但请注意,这里的圆心角需要用弧度来表示,而不是度数。弧度是一个在角度测量中使用的单位,它与圆的半径长度有关。一个完整的圆对应的弧度是2π,因此,扇形的圆心角在弧度制下介于0到2π之间。
虽然用弧长计算扇形面积的方法稍微复杂一些,但它同样非常实用。扇形面积的另一种计算公式是:扇形面积 = (1/2) × 弧长 × r。这个公式利用了扇形面积与弧长和半径之间的几何关系,让我们可以通过已知的弧长和半径来求解面积。
假设我们有一个弧长为5π厘米,半径为3厘米的扇形。要计算它的面积,我们只需要将弧长5π厘米和半径3厘米代入公式。所以,扇形面积 = (1/2) × 5π × 3 = 7.5π平方厘米,约等于23.55平方厘米。
现在,你已经掌握了两种计算扇形面积的方法,是不是觉得扇形其实并没有那么神秘了呢?当然,学习是一个不断巩固和提升的过程。为了帮助你更好地理解和运用这些公式,下面提供一些实用的技巧和注意事项:
1. 明确已知条件:在开始计算之前,先仔细审题,明确题目给出的已知条件。是圆心角和半径?还是弧长和半径?根据已知条件选择合适的公式进行计算。
2. 单位换算:如果题目中给出的圆心角是度数而不是弧度,记得先将其转换为弧度再进行计算。同样地,如果弧长的单位是厘米而半径的单位是米,也需要先进行单位换算。
3. 灵活运用公式:在实际应用中,你可能会遇到一些复杂的情况,比如需要计算多个扇形的总面积或者扇形的部分面积。这时,你需要灵活运用公式,结合题目中的条件进行求解。
4. 检查答案:计算完成后,别忘了检查你的答案是否合理。比如,扇形面积应该是一个正数;如果计算出的面积比整个圆的面积还大,那么很可能是你的计算过程出了问题。
5. 实践应用:学习扇形面积的计算不仅仅是为了应对考试或作业,更重要的是能够将其应用到实际生活中去。比如,在设计蛋糕时,你可以通过计算扇形面积来确定每个部分的尺寸;在物理学中,扇形面积的概念也可以用来解释一些复杂的物理现象。
通过这篇文章,相信你已经对扇形面积的计算有了更深入的了解。记住,数学是一门需要不断练习和思考的学科。只有不断尝试、不断挑战自己,你才能真正掌握这门学科的精髓。所以,不妨现在就拿起笔来,找一些相关的练习题进行练习吧!相信在不久的将来,你一定会成为扇形面积计算的高手
- 上一篇: 如何在论文目录中正确添加点点(省略号)?
- 下一篇: 谷歌浏览器翻译网页,一键搞定!
-
 建筑面积与使用面积换算技巧资讯攻略10-29
建筑面积与使用面积换算技巧资讯攻略10-29 -
 深圳二手房购房需要缴纳哪些税费?资讯攻略12-01
深圳二手房购房需要缴纳哪些税费?资讯攻略12-01 -
 二手房过户费用计算器及计算方法资讯攻略11-26
二手房过户费用计算器及计算方法资讯攻略11-26 -
 二手房交易税费计算指南资讯攻略11-02
二手房交易税费计算指南资讯攻略11-02 -
 揭秘!羽毛球场地标准尺寸:究竟占据了多少平方米的激情空间?资讯攻略10-28
揭秘!羽毛球场地标准尺寸:究竟占据了多少平方米的激情空间?资讯攻略10-28 -
 DIY壁纸贴法:详细步骤教你轻松上手资讯攻略11-17
DIY壁纸贴法:详细步骤教你轻松上手资讯攻略11-17












