初三数学中黄金分割公式的口诀是什么?
初三数学是学生们在学习生涯中面临的一个重要阶段,特别是在几何和代数领域,学生们需要掌握各种公式和口诀来提高解题效率和准确性。其中,黄金分割公式作为一个经典而有趣的数学概念,不仅在数学学科中占据重要地位,还广泛应用于建筑、艺术和设计等领域。为了帮助大家更好地理解和记忆这一公式,下面将详细介绍初三数学中的黄金分割公式及其口诀。

黄金分割的定义起源于古希腊数学家毕达哥拉斯学派,它指的是将一个线段分割为两段,使得整个线段与较长部分的长度之比等于较长部分与较短部分的长度之比。这一比例被记为“黄金比例”或“神圣比例”,通常用希腊字母φ(phi)表示,其近似值为1.618。在数学上,黄金分割具有独特的性质,如自相似性、无穷嵌套等,使得它成为美学和设计中备受推崇的比例。

具体到初三数学中,黄金分割公式可以表示为:若一条线段的总长度为a+b(a为较长部分,b为较短部分),则a/b=φ,或(a+b)/a=φ。这个公式看似简单,但在实际应用中却非常灵活多变。为了帮助学生更好地记忆和运用这一公式,我们可以借助口诀来加深印象。

口诀一:“长段比短段,比值一点六。”
这句口诀直接点明了黄金分割的核心,即较长部分与较短部分的比值约为1.618(简化为1.6以方便记忆)。通过这个口诀,学生可以迅速联想到黄金分割的基本性质,为解题打下基础。
口诀二:“整体比长段,比值仍是一点六。”
这句口诀进一步扩展了黄金分割的应用范围,指出整个线段与较长部分的比值也约为1.618。这有助于学生理解黄金分割的递归性和自相似性,为处理更复杂的几何问题提供思路。
口诀三:“黄金分割真奇妙,建筑艺术离不了。”
这句口诀从实际应用的角度出发,强调了黄金分割在美学和设计中的重要性。通过提及建筑和艺术领域的应用,学生可以更加直观地感受到黄金分割的魅力和实用性,从而激发学习兴趣和动力。
接下来,我们结合一些具体例题来展示如何运用黄金分割公式和口诀进行解题。
例题一:已知一条线段的总长度为10厘米,其中较长部分的长度为6.18厘米,求较短部分的长度。
解题思路:根据黄金分割公式a/b=φ,我们可以将已知条件代入公式进行计算。设较短部分的长度为b,则有6.18/b=1.618(或近似为1.6)。解这个方程,我们可以得到b的值为3.82厘米(或近似为4厘米,取整数便于理解)。通过验证,我们可以发现6.18与3.82的比值确实接近黄金比例1.618,从而验证了答案的正确性。
例题二:一个矩形的长为16厘米,宽为10厘米。请问这个矩形的长宽比是否接近黄金比例?如果不接近,应该如何调整宽度以使其接近黄金比例?
解题思路:首先,我们计算矩形的长宽比,即16/10=1.6。这个比值与黄金比例1.618非常接近,但仍有微小的差距。为了使其更接近黄金比例,我们可以根据黄金分割公式进行调整。设新的宽度为x厘米,则有16/x=1.618。解这个方程,我们可以得到x的值为9.9厘米(保留一位小数)。因此,我们可以将矩形的宽度调整为9.9厘米,以使其长宽比更接近黄金比例。
通过这两个例题,我们可以看到黄金分割公式在解决实际问题中的灵活性和实用性。同时,口诀的运用也极大地提高了学生的记忆效率和解题速度。
除了以上介绍的口诀和例题外,还有一些其他的方法可以帮助学生更好地理解和掌握黄金分割公式。例如:
1. 画图辅助理解:通过绘制线段图或矩形图等几何图形,学生可以直观地看到黄金分割在图形中的应用和表现。这有助于加深他们对公式的理解和记忆。
2. 实际测量应用:鼓励学生在实际生活中寻找黄金分割的例子进行测量和分析。比如:测量建筑物的高度和宽度、艺术作品的长宽比等。通过实际操作和观察,学生可以更加深入地理解黄金分割的实用性和美学价值。
3. 小组讨论交流:组织学生进行小组讨论或合作学习活动,让他们相互分享自己对黄金分割公式的理解和应用经验。通过交流和互动,学生可以拓宽思路、发现问题并共同解决难题。
总之,初三数学中的黄金分割公式是一个既重要又有趣的概念。通过掌握相关的口诀和解题方法,学生可以更加轻松地理解和运用这一公式。同时,通过实际应用和小组讨论等方式的学习活动,学生还可以进一步加深对黄金分割的理解和认识。希望这篇文章能够为大家在学习黄金分割公式方面提供一些有益的帮助和启示。
- 上一篇: 揭秘:千纸鹤背后的禁忌,为何不宜赠与他人?
- 下一篇: 如何编织四股辫?
-
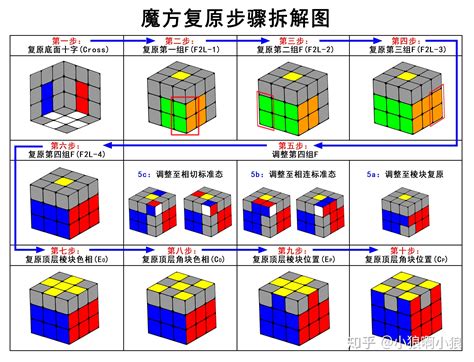 六面魔方还原的最简单口诀或方法是什么?资讯攻略10-24
六面魔方还原的最简单口诀或方法是什么?资讯攻略10-24 -
 如何转六面魔方并完成十字架?口诀是什么?资讯攻略11-12
如何转六面魔方并完成十字架?口诀是什么?资讯攻略11-12 -
 Word中如何输入分数资讯攻略12-06
Word中如何输入分数资讯攻略12-06 -
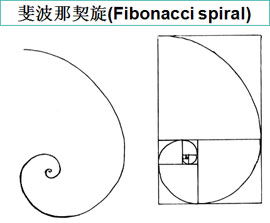 如何绘制黄金分割比例资讯攻略12-03
如何绘制黄金分割比例资讯攻略12-03 -
 Word中轻松输入分数的方法资讯攻略11-02
Word中轻松输入分数的方法资讯攻略11-02 -
 轻松学会在Word文档中插入分数的方法资讯攻略12-02
轻松学会在Word文档中插入分数的方法资讯攻略12-02












